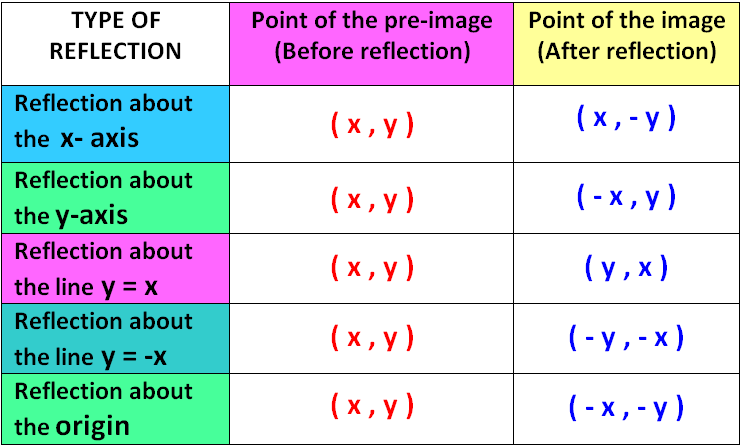
$\begingroup$ Reflecting a function along the line y = x is the same as computing the inverse of the function So use a method for computing the inverse of a function to find the reflection about the line y = x $\endgroup$ – user10 Feb 18 ' at 2123 How do you prove that the point P (x,y) becomes P' (y,x) after reflecting upon the line y=x?Thus for y = f ( x), the reflection about the line y = x is accomplished by x = f ( y) For example, the reflection about the line y = x for y = x 2 is the equation x = y 2 Hope it helps If the curve is complicated, you can just take particular, interesting points and switch the coordinates

Reflection In The Line Y X Transformation Matrix Youtube
Reflection in line y=x worksheet
Reflection in line y=x worksheet- Reflection Over the XAxis For our first example let's stick to the very simple parent graph of y = x^2 {See video for graph} On the screen you can see that the graph of this equation is a parabola The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)




Reflection Over Y 2 With Rule Educreations
1 Start by rearranging the equation of the mirror line into 2 3x − y = − 8 3 The normal form of the equation of a line is n ⋅ x = const, where n is some vector normal (perpendicular) to the line Comparing this to the mirror line equation, I see that a normal to it is (2 3, − 1) Since any normal will do, I'll multiply this by − 3Reflection line points ShareReflect over the line y = x answer choices (2, 4) (4, 2) (4, 2) (4, 2) s Question 18 SURVEY 30 seconds Q The preimage is _____ to the image in a reflection answer choices similar congruent s Question 19 SURVEY 30 seconds Q Is a reflection an isometry?
The line of reflection will lie directly inWhen you reflect over xaxis the coordinates are (x,y) and when you reflect over the yaxis the coordinates are (x,y If you want to reflect over y=x then the coordinates are (y,x) If you want to reflect over y=x the coordinates are (y,x) Comment on Caylen Jang's post "You can use aThe line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I wi
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xPrecalculus 1 Answer Jim G image A' = (5 , 3 ) Explanation Any point (x , y ) when reflected in the line y = x has an image ( y , x ) example A (3 , 4 ) has image A' ( 4 , 3 ) Answer link Related questionsApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the




Kite Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection Brainly Com




In The Xy Coordinate Plane Point P Is The Reflection Of The Point With Coordinates 3 1 Across The Line Y X Point T Is The Reflection Of Point P Across The Y Axis What
To reflect along a line that forms an angle θ with the horizontal axis is equivalent to rotate an angle − θ (to make the line horizontal) invert the y coordinate rotate θ back Further, y = mx implies tanθ = m, and 1 m2 = 1 cos2θ Then, assumming you know about rotation matrices, you can writeReflection about the line y = x Reflecting over Any Line When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure In other words, the line x = 2 (line of reflection) lies directly in the middleFinding the inverse from a graph Your textbook probably went on at length about how the inverse is "a reflection in the line y = x"What it was trying to say was that you could take your function, draw the line y = x (which is the bottomleft to topright diagonal), put a twosided mirror on this line, and you could "see" the inverse reflected in the mirror




Reflections Through The Axes And The Lines Y X And Y X Geogebra
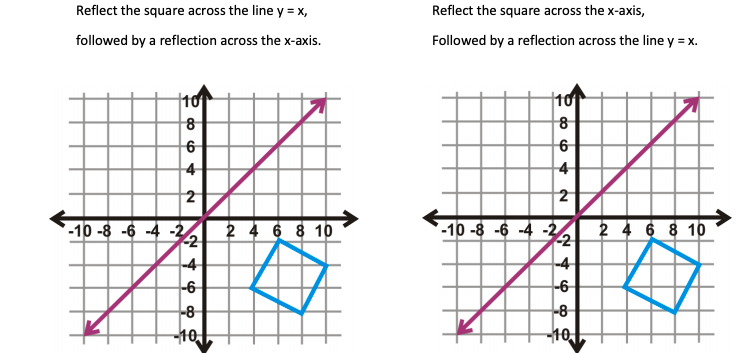



Reflect The Square Across The Line Y X Followed By Chegg Com
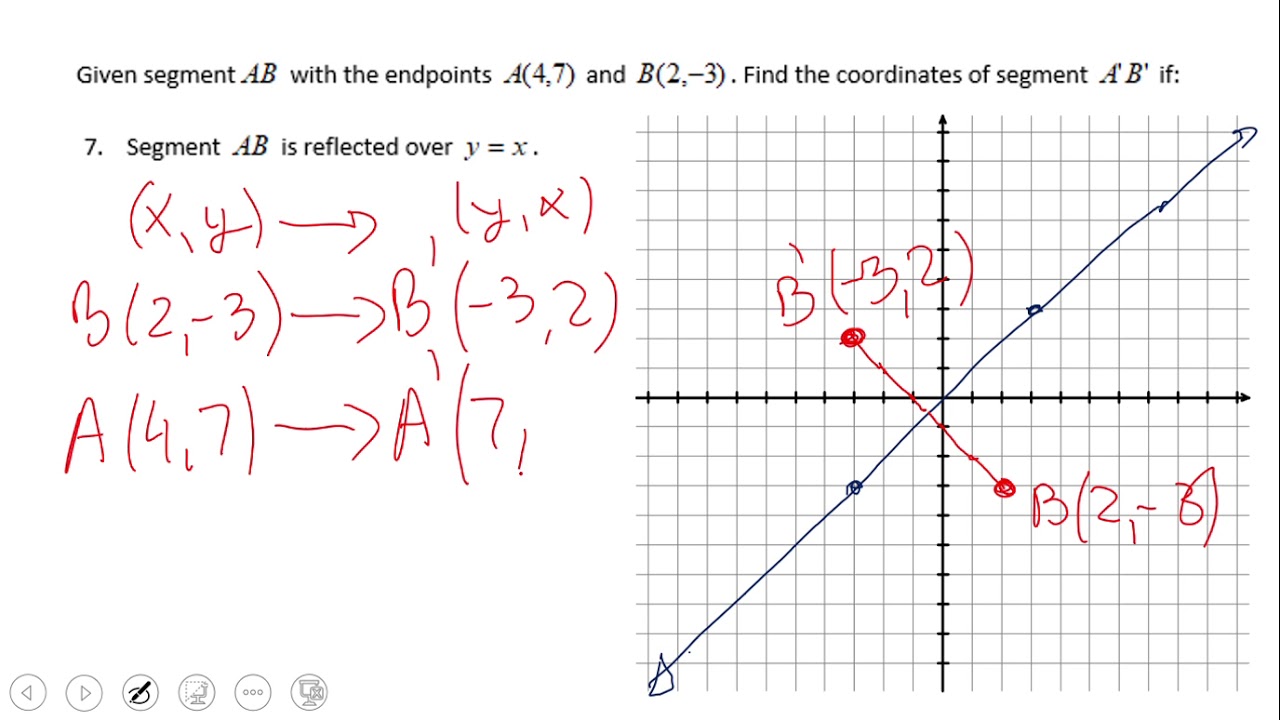
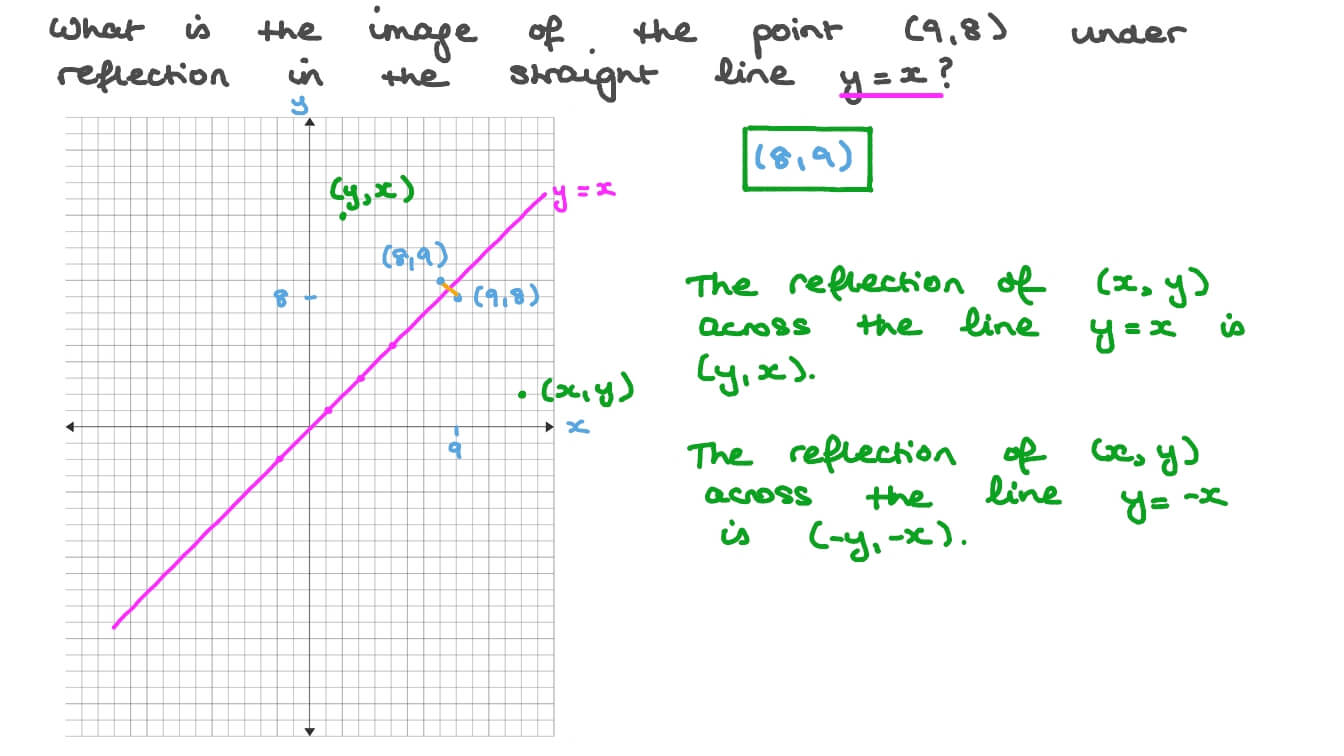
The problem is asking us to reflect the point (8, 7) over the reflection line y = x We will follow the method described in the below video (this guy Stepbystep explanation Under a reflection in the line y = x a point (x, y ) → (y, x ) , thus (8, 1 ) → ( 1, 8 ) kason11wd and 4 more users found this answer helpful heart outlined Thanks 3 star starReflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Geometry Transformations
Reflection over the line y = x Which rigid motion maps A(3, 1) to A'(1, 3)?This lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitterThe line y = x is the point ( y, x ) Reflect over any line Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure The line of reflection will lie directly in the middle between the original figure and its image




Reflections Ck 12 Foundation



1
A point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxisFor a point reflection, we actually reflect over a specific point, usually that point is the origin $ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red a , \red b) $ O a reflection through the origin O a reflection over the line y = x O a dilation with a scale factor of 1 centered at (2,3) a dilation with a scale factor of centered at the origin Categories English Leave a Reply Cancel reply Your email address will not be published Required fields are marked *Graph the line Ask students to start with point A and reflect it over the line My students told me to go left 2 squares to get to y = xx and then 2 more squares past that to create the new line While this is the method we learned for reflecting points over a line, we always had a horizontal or vertical line, not a diagonal line




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflection In The Line Y X Transformation Matrix Youtube
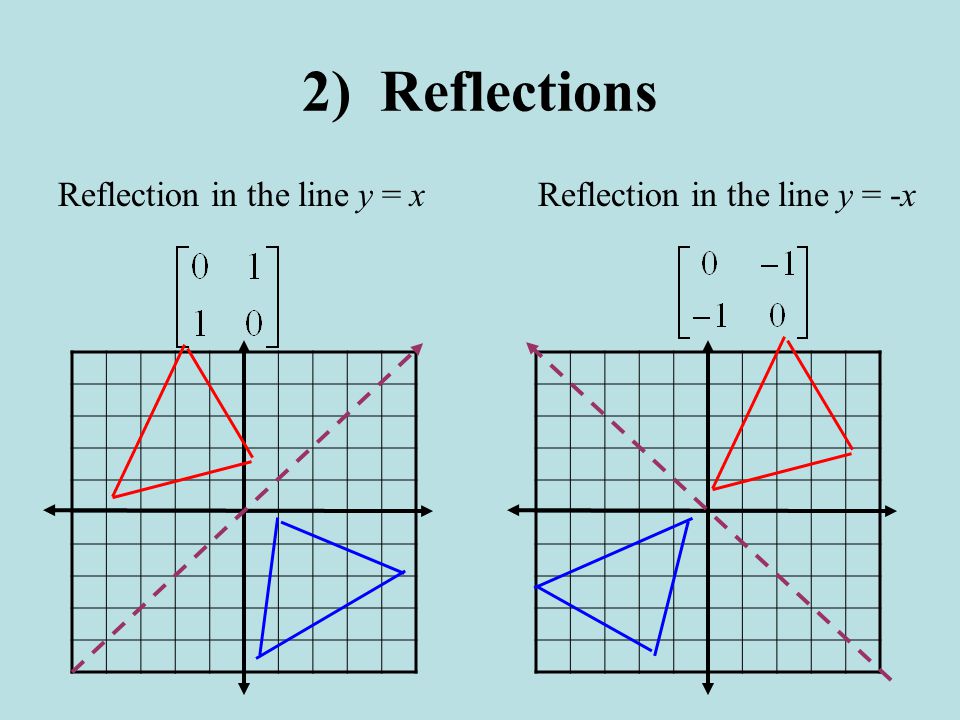
Reflection in a Line 4 Reflecting over the line y = x or y = x (the lines y = x or y = x as the lines of reflection) When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change placesA shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x The point A has Cartesian coordinates (−3, 5) The reflected point A' has Cartesian coordinates (−5, 3) The xcoordinate of A (−3) has its sign changed (3) and becomes the ycoordinate of A'2 See answers itsA rlara812 rlara812 Answer a Stepbystep explanation what ever this my big brothers computr i don't care i am trying to help peoplenotstealpoints getout no!




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Geogebra Project Rotations And Reflections Math At Dis
A reflection is a "flip" of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection Reflection in the line y = 0 ie, in the xaxis The line y = 0 means the xaxis Let P be a point whose coordinates are (x, y) Therefore, when a point is reflected in the xaxis, the sign of its ordinate changesGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha




02 02 Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Brainly Com




Ixl Reflections Find The Coordinates Grade 7 Maths Practice
This brief video explores reflecting an image over the y=x and the y=x lines, with the coordinate rules for both180˚ rotation about the origin (clockwise or counterclockwise would give you the same result)First you have to get the perpendicular s(x) = ms ⋅x t s ( x) = m s ⋅ x t (the dashed red line) You have to know this ms = − 1 m m s = − 1 m And then you know that P P is on s s So you simply put in the values x,y x, y of P and solve to t t t = y−ms ⋅x t = y − m s ⋅ x Now you have s s As s s and g g have exactly point




How To Find A Reflection Image



Reflection Of A Point In A Line Assignment Point
Geometry 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflect over x= 1 reflection over the line y=x Reflection over y=x reflection over yaxis reflectionFor example, when reflecting the point (2,5) over y=x it becomes (5,2) This is very simple, but why does it work?Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)




Introduction And Review Information Ppt Video Online Download




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
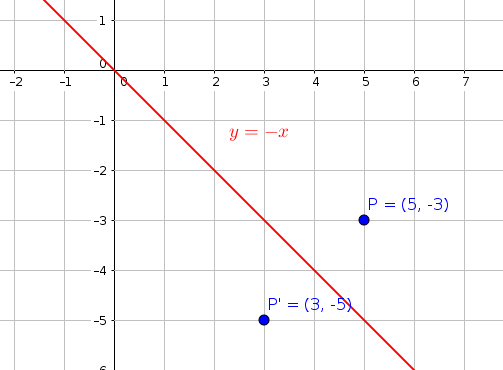
is mapped to (x',y') by a reflection in the line X = 2 we note (1) the ycoordinate is unaffected (2) for reflections the distance from the line of reflection to the object is equal to the distance to the image point ∴ a = 2 2 = 4units so the image point is 4 units from the line of reflection ie x' = 2 4 = 6Reflection over the line y = − x A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = − xLeave kid youreannoyingeveryone 1coryphaeus1 1coryphaeus1
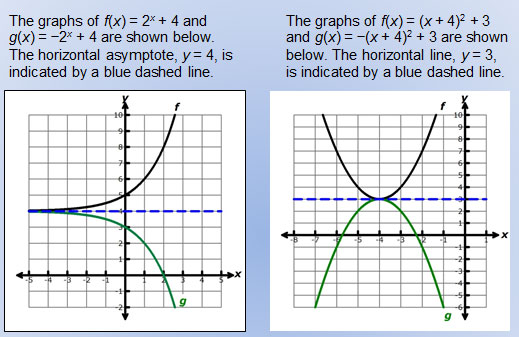



Untitled Document




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
What is #A'#, the image of #A(3,5)#, after a reflection in the line #y = x#?The rule for a reflection in the line y = x is ( x , y ) → ( y , x ) Reflection in the line y = − x A reflection of a point over the line y = − x is shown The rule for a reflection in the origin is ( x , y ) → ( − y , − x Which image is a reflection over the line y = x of triangle 1?



2



1 Geometry Ms Singarajah 7
Reflect over y=x The reflection of the point (x,y) across the line y=x is the point (y,x) Reflect over y=x The reflection of the point (x,y) across the line y=x is the point (y,x) Where will the line of reflection lie?What is the image of (9,3) after a reflection over the line y=x 1 See answer kingtee03 is waiting for your help Add your answer and earn points rani rani Answer (3,9) Stepbystep explanation line segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line




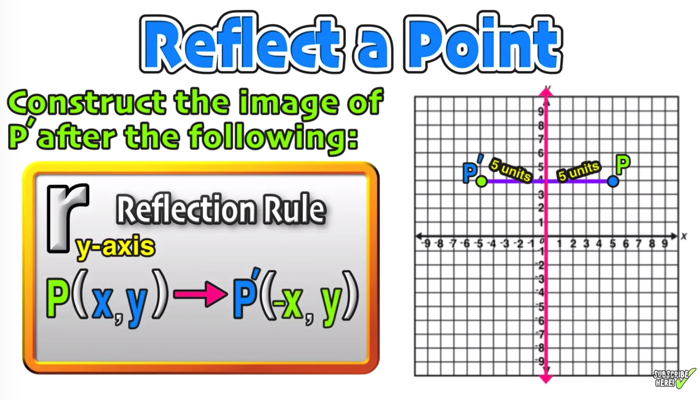
What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflection Over The Line Y X Geogebra
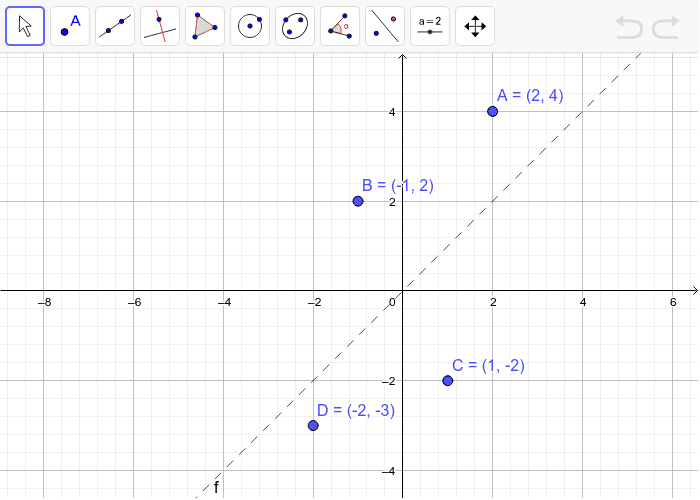
90˚ counterclockwise rotation about the origin OR 270˚ clockwise rotation about the origin Which rigid motion maps A(3, 1) to A'(3, 1)?Reflection, Geometric Transformations Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinates How do they relate to each other?Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =



Assignment 2 Transforming Parabolas




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
Tutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT



Http Www Dentonisd Org Cms Lib Tx Centricity Domain 11 Chpt9notes Pdf




Reflection Mathbitsnotebook A1 Ccss Math




Reflection




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Tbaisd Moodle
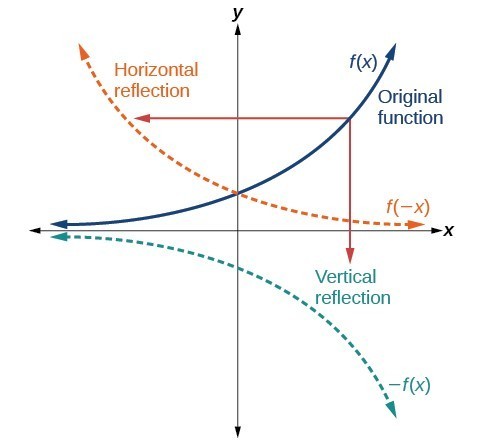



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




Reflection Over Y X Math Geometry Showme



What Is The Image Of 2 5 Reflected Across X 2 Socratic




10 Math Problems Transformation Reflection
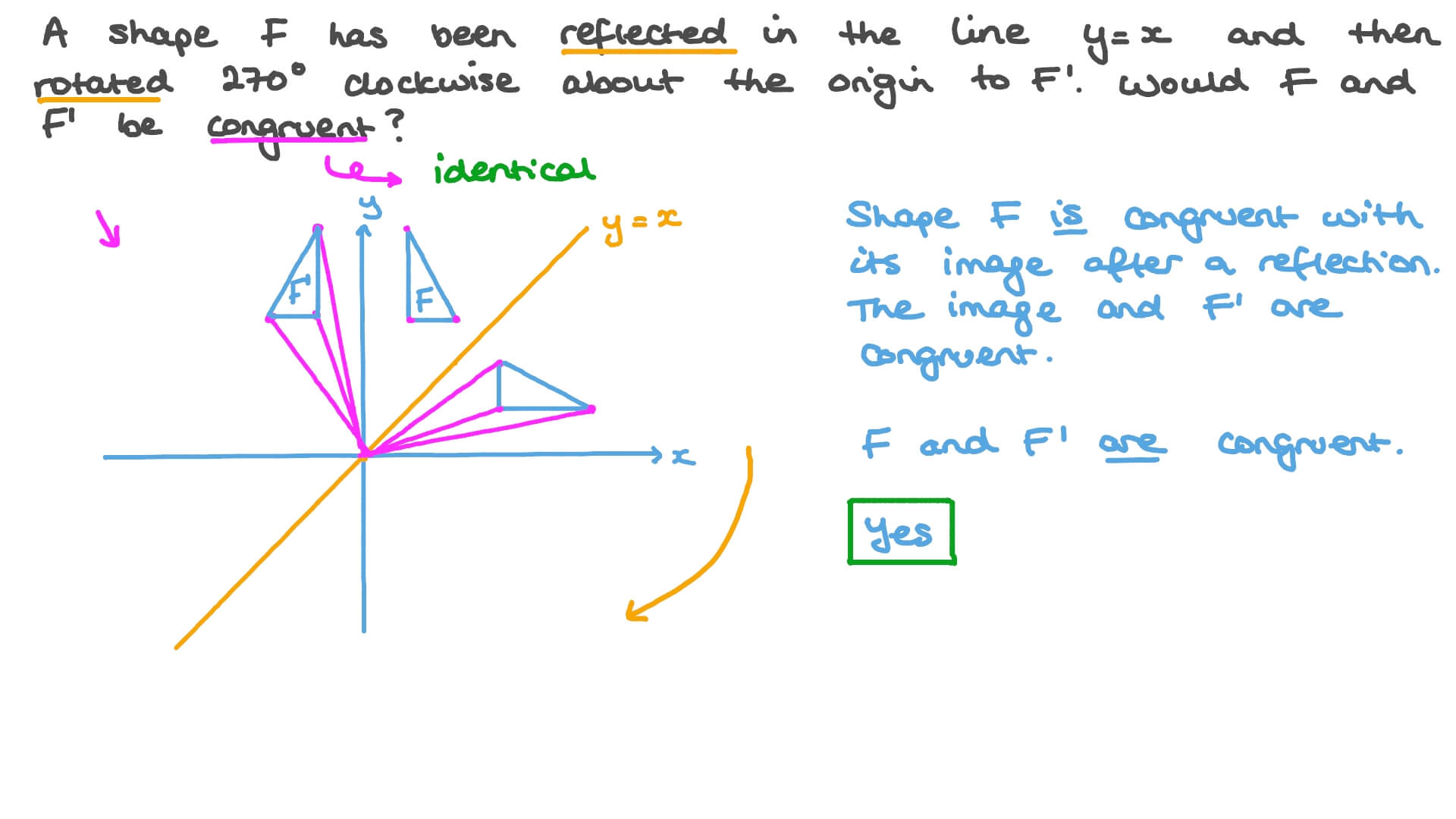



Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa



1




Reflecting Functions Examples Video Khan Academy




Learn About Reflection Over The Line Y X Caddell Prep Online
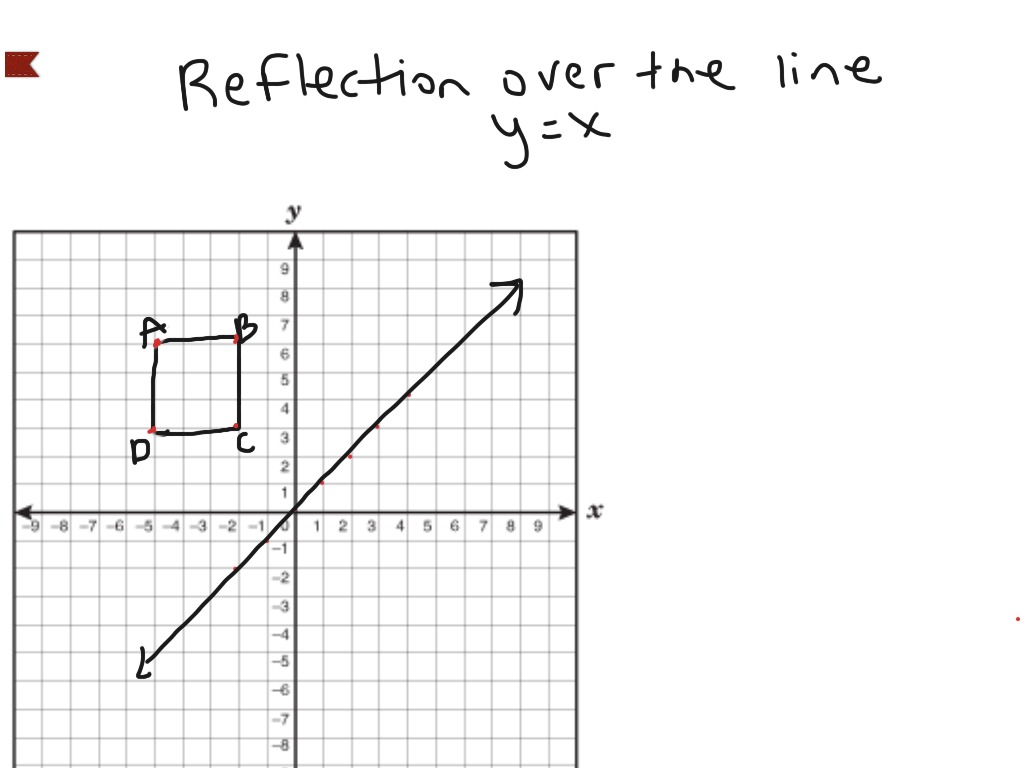



Reflection Over The Line Y X Math Showme



Search Q Coordinate Plane Tbm Isch
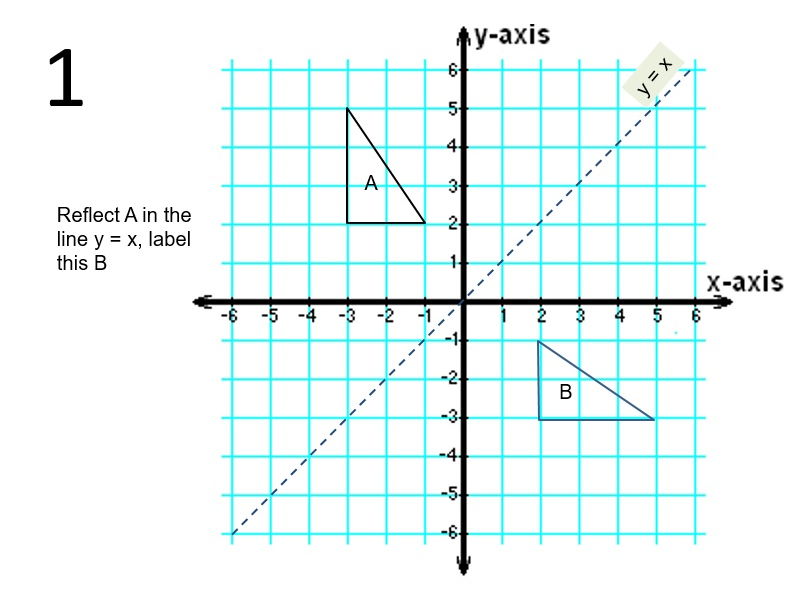



Diagonal Reflections In The Line Y X Teaching Resources




Picture Of Reflection In The Line Y X Reflection Math Math Reflection




Reflection Definition Reflection In The Coordinate Plane




Reflection Mathbitsnotebook A1 Ccss Math
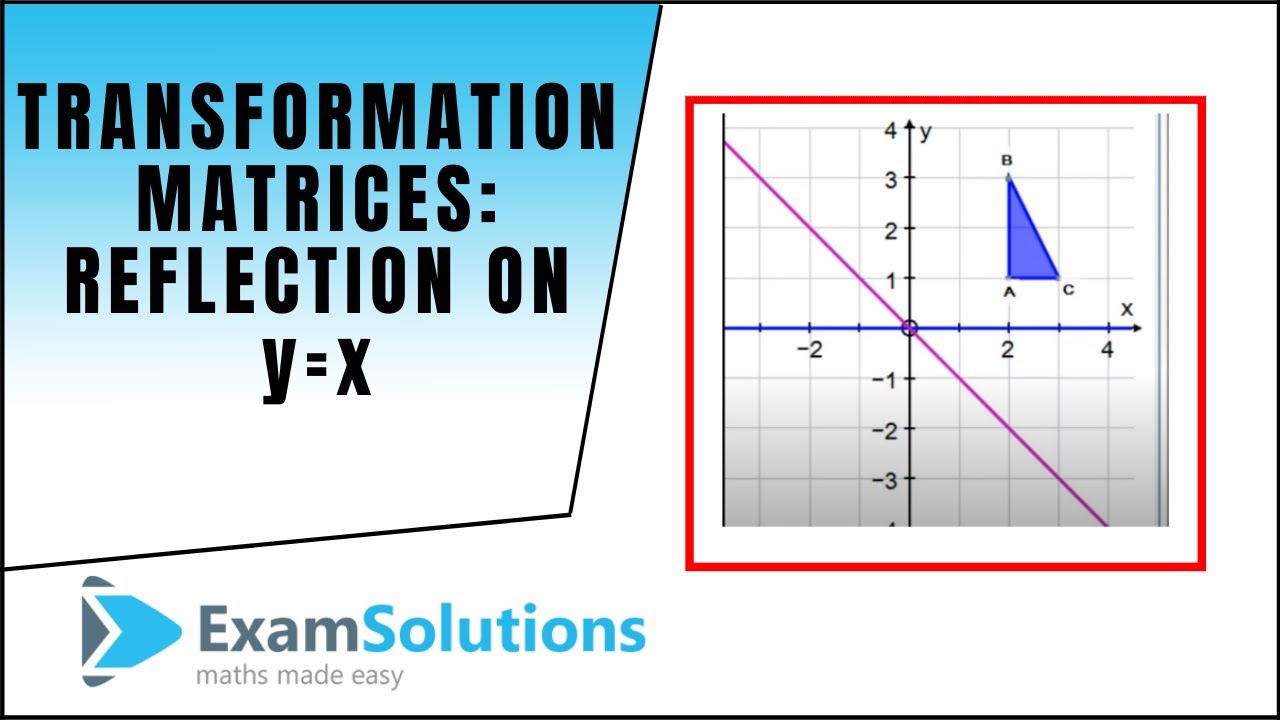



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



Reflection Transformation




Transformations Boundless Algebra




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




What Is A Line Of Reflection Printable Summary Virtual Nerd




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora




How To Find A Reflection Image



What Is The Reflection Image Of 5 3 In The Line Y X Socratic




Reflection In The Line Y X Geogebra




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over Y X And Y X Youtube



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com



Reflecting In The Line Y X 2 Geogebra




Reflections Ck 12 Foundation



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com




Reflection Transformation Matrix




Transformation Reflection Over The Line Y X Youtube



Math Alive Geometry 1




Reflection Transformation Matrix




Transformations Of Graphs



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative




Reflection Over The Y X Line Youtube
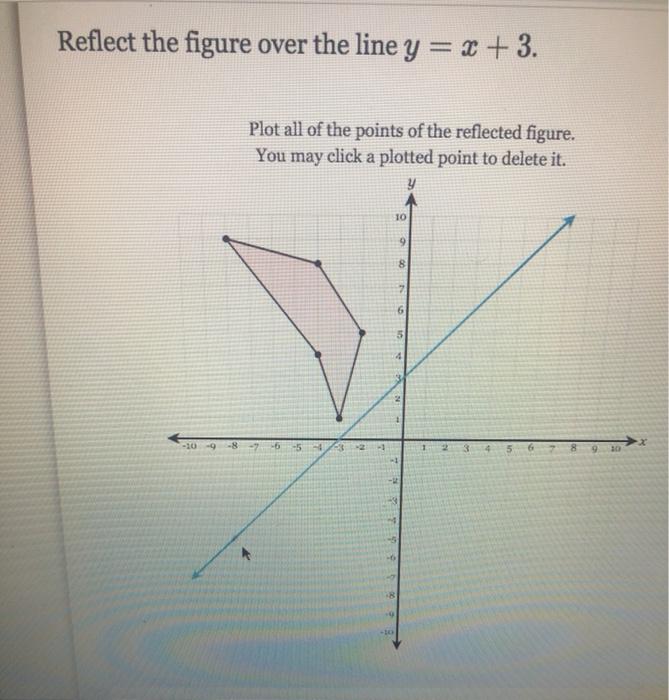



Reflect The Figure Over The Line Y X 3 Plot All Chegg Com



Math Alive Geometry 1




Reflection Over The Line Y X Math Showme
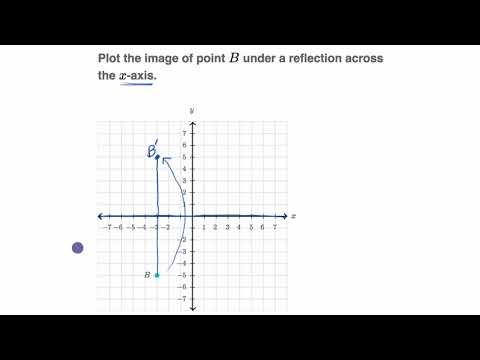



Reflecting Points Video Reflections Khan Academy




Reflection Over A Line Expii
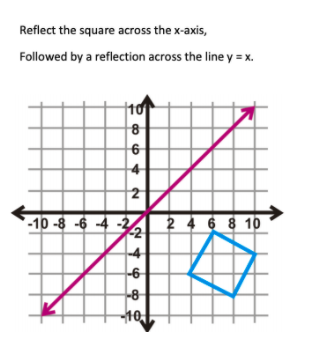



Reflect The Square Across The X Axis Followed By A Chegg Com



1



What Does It Mean To Reflect Over The Y X Line Quora
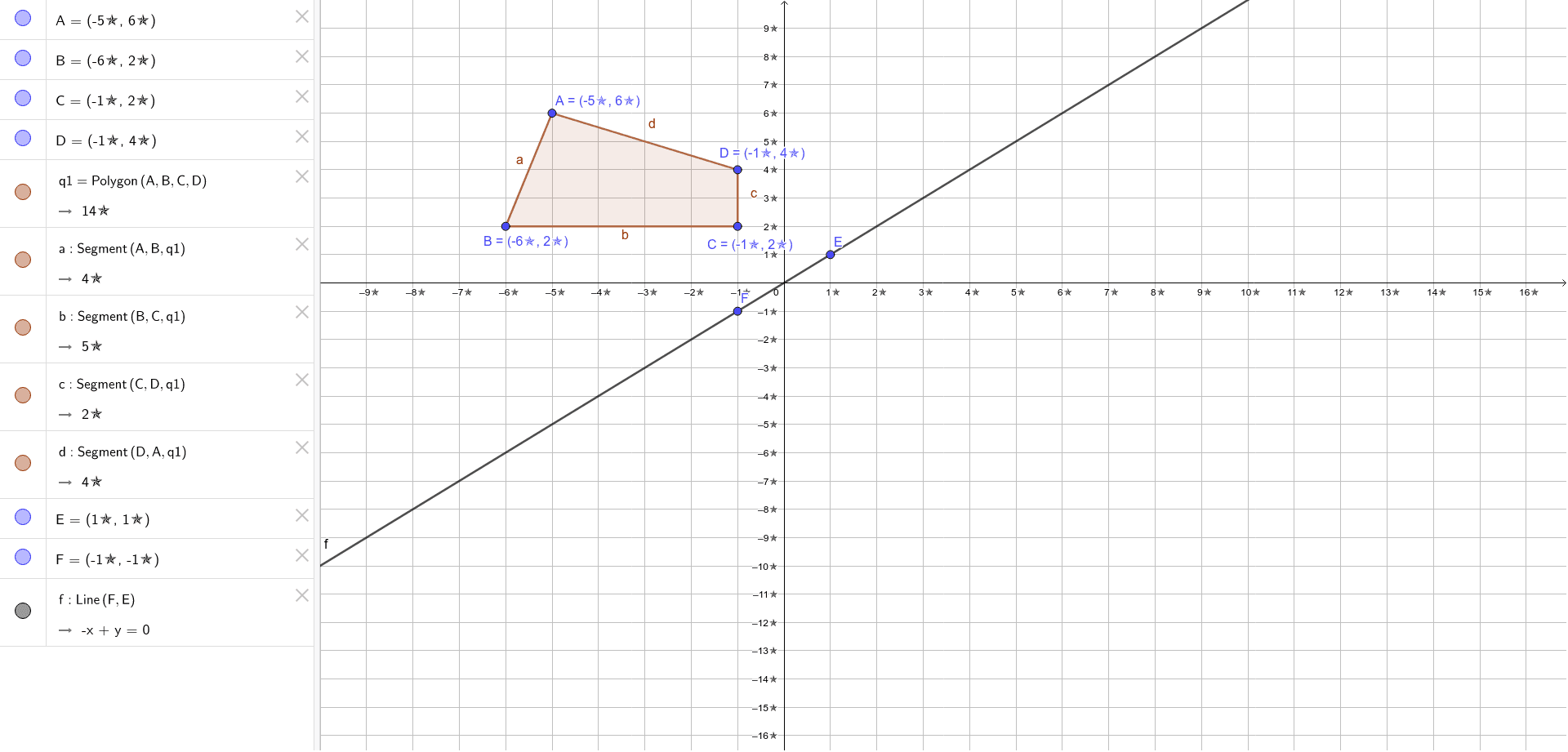



Reflection Across The Line Y X Geogebra
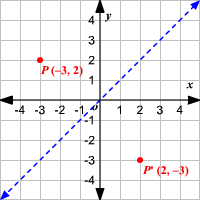



Reflections
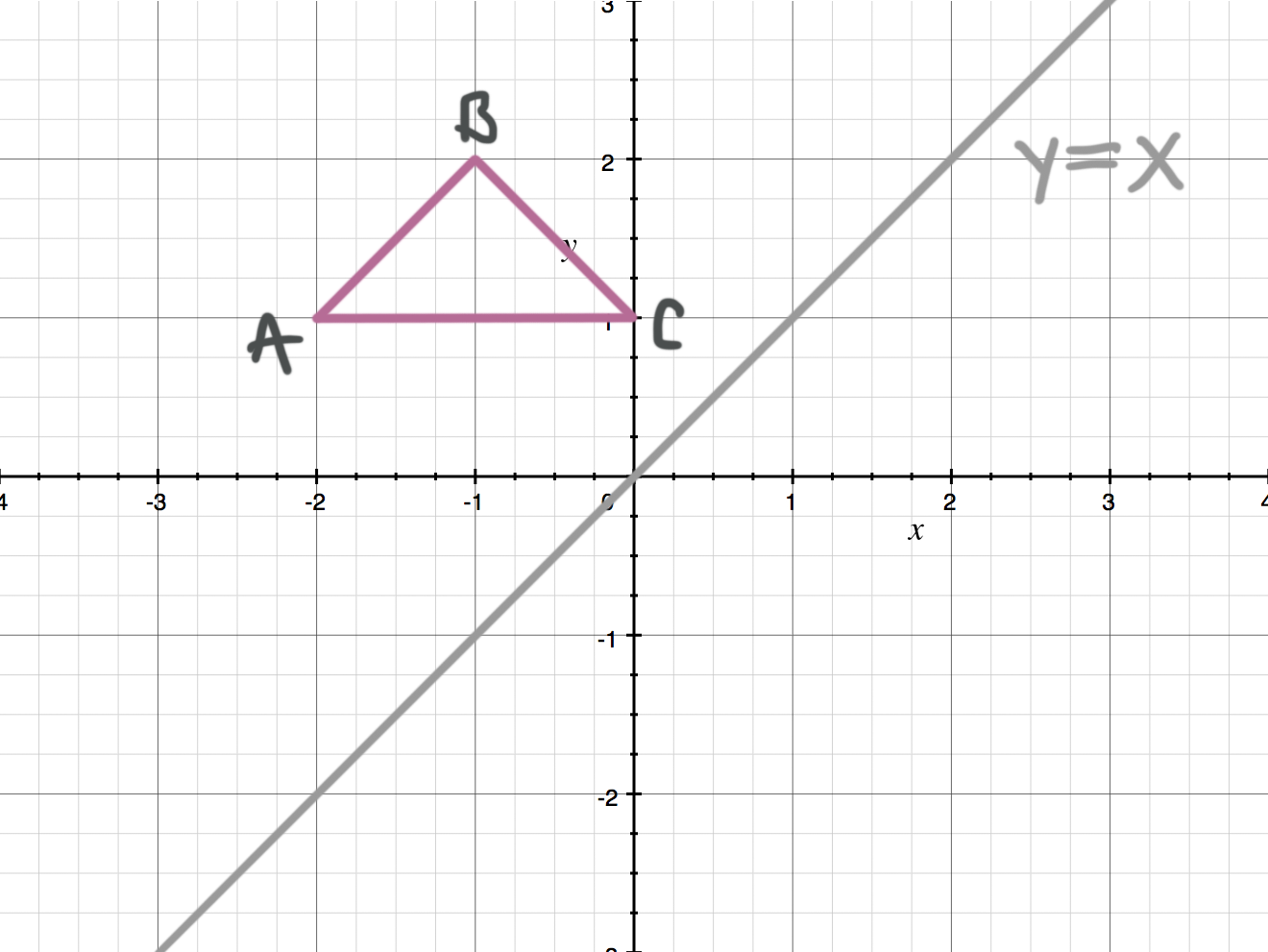



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q
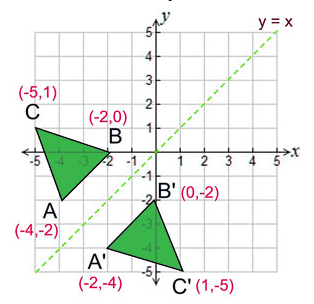



Reflection Definition Reflection In The Coordinate Plane




Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
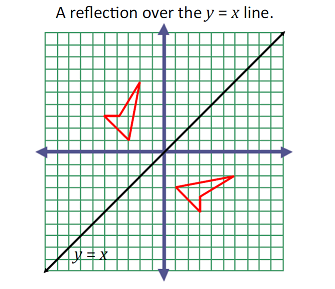



Great Minds Eureka Math Blog




Reflection Over Y 2 With Rule Educreations



Solution What Is The Image Of A 3 1 After A Reflection First Across The Line Y 3 And Then Across The Line X 1



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N




Algebraic Representations Of Reflections



Illustrative Mathematics




Reflection Over The Line Y X Youtube




How To Reflect A Graph Through The X Axis Y Axis Or Origin
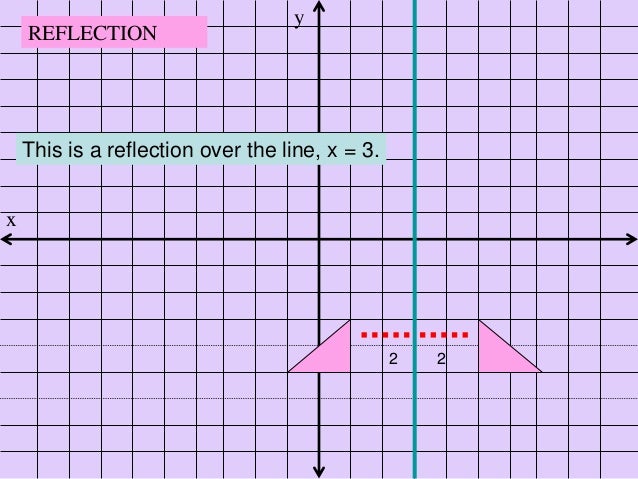



Reflections
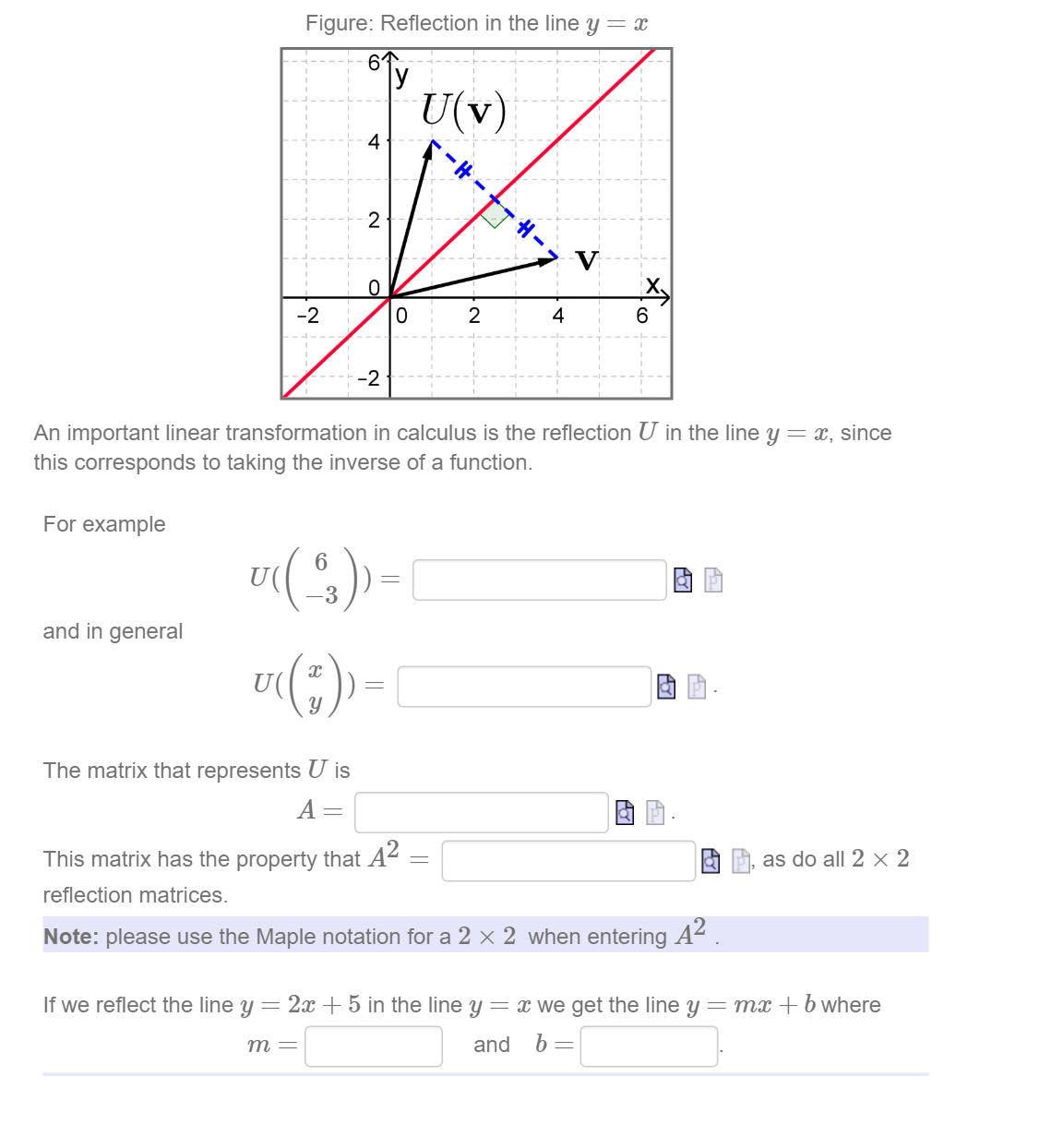



An Important Linear Transformation In Calculus Is The Chegg Com




Reflections Across Y X Geogebra
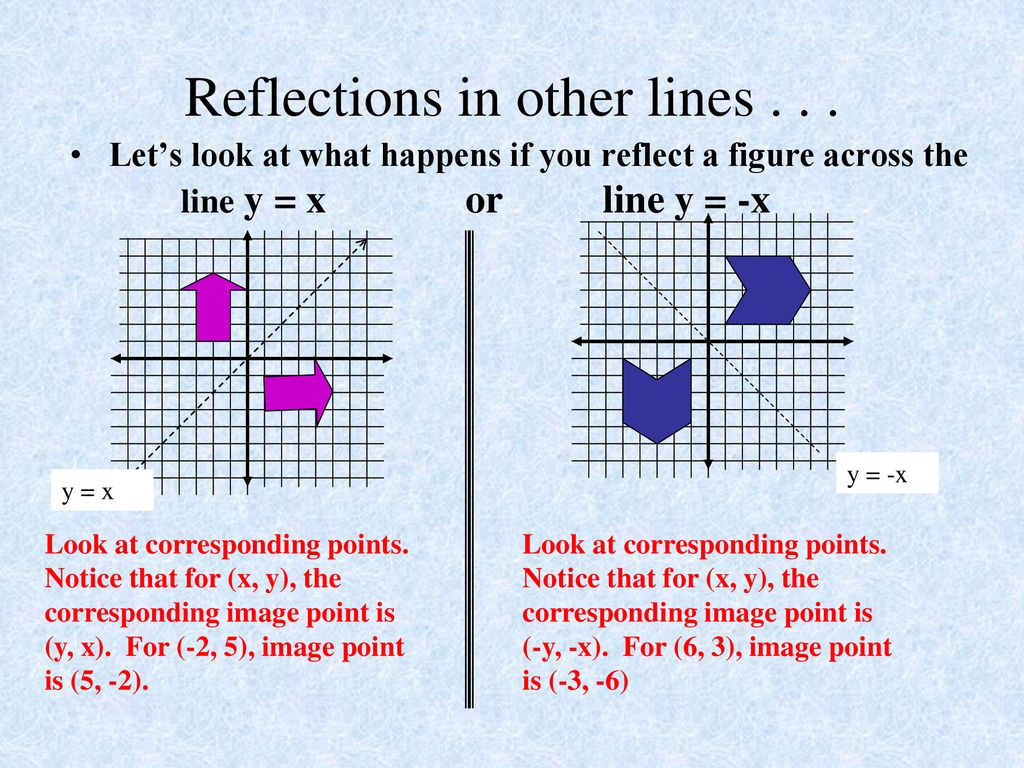



Transformations Dilations Translations Reflections Rotations Ppt Download




How To Reflect A Graph Through The X Axis Y Axis Or Origin



Geometric Reflections Q35 50 Intro To Geometry




Picture Of Reflection Across Y Axis Reflection Math Reflection Math



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Write The Coordinates Of The Vertices After A Reflection Across The Line Y X Brainly Com




Common Reflections Key Stage 3




Ppt Reflect Over Y X Powerpoint Presentation Free Download Id



4 4 Transformations With Matrices Ppt Video Online Download



0 件のコメント:
コメントを投稿